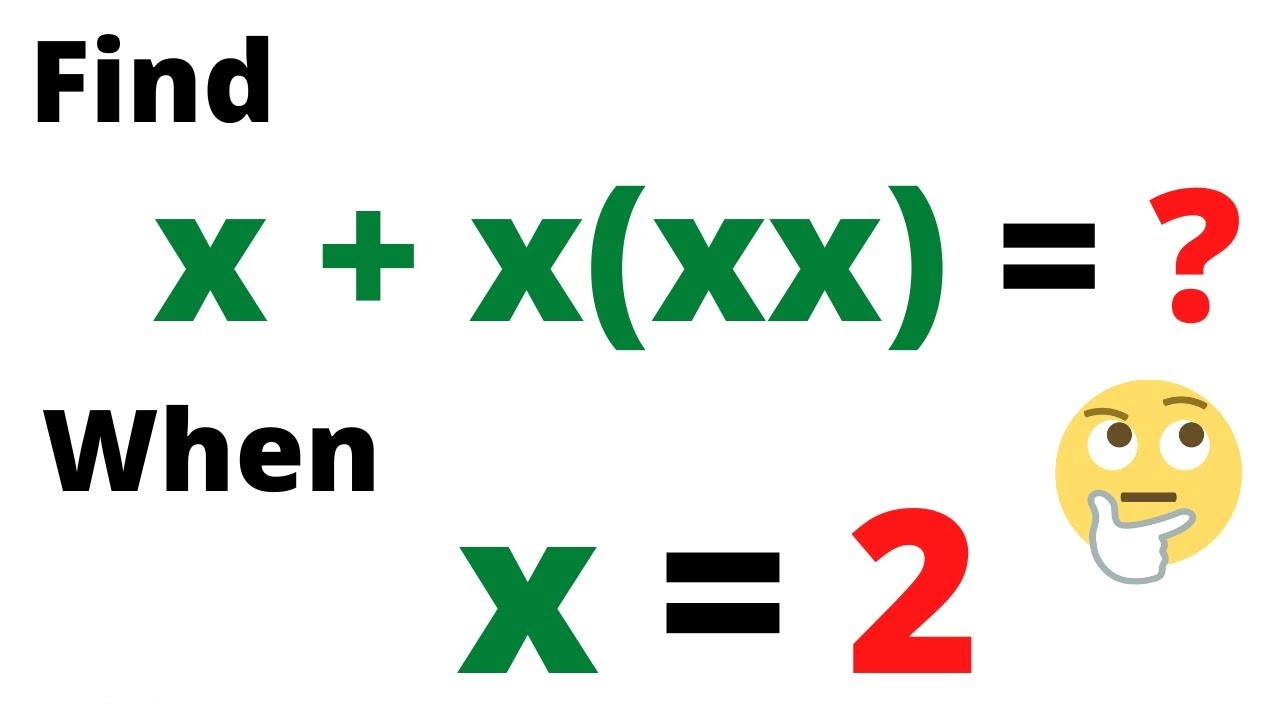What is x when x * x * x is equal to 2? A Clear Guide to ∛2 ≈ 1.25992
When solving the equation x * x * x = 2, we’re looking for the number that, when multiplied by itself three times, equals 2. In mathematical terms, this is known as the cube root of 2, written as ∛2 or 2^(1/3).
The answer is approximately
🔹 x ≈ 1.259921
It’s important to note:
- This is an irrational number — it has an infinite number of non-repeating decimal places.
- It cannot be expressed as an exact fraction.
📐 What Is a Cube Root?
The cube root of a number is the value that, when used in a multiplication three times, gives that number.
So:
- ∛2 = x
- x·x·x = 2
- x ≈ 1.25992
Like √2 gives us a square root, ∛2 provides us with the cube root of 2.
🔢 How Do You Find the Cube Root of 2?
1. Estimation by Averaging (Manual Method)
You can estimate the cube root using a trial-and-error average approach.
Example:
- Start with two close numbers: 1 and 2.
- Try 1.3 → 1.3³ = 2.197
- Try 1.2 → 1.2³ = 1.728
- Narrow between them → try 1.26 → 1.26³ = 2.00037
This method can be refined repeatedly for more precision.
2. Using a Calculator
Most calculators will give
∛2 ≈ 1.25992104989…
📚 Why Is ∛2 an Irrational Number?
The number ∛2 cannot be expressed as a fraction (like 3/2 or 7/5). That makes it irrational, just like π or √2.
It’s not a repeating decimal and never terminates.
Mathematicians have proven that there’s no pair of integers a/b that satisfy (a/b)³ = 2.
🧭 Historical Insight: Doubling the Cube
In ancient Greek mathematics, the famous “doubling the cube” problem asked:
“Can you construct the cube root of 2 using only a compass and straightedge?”
Answer: No.
This was one of the earliest challenges that revealed limitations in classical geometric construction. It also introduced the concept of irrational cube roots.
🎯 Common Mistakes to Avoid
❌ Confusing with square root: Remember, ∛2 ≠ √2 (∛2 ≈ 1.26, but √2 ≈ 1.41)
❌ Incorrect exponent rules: (2)^(1/3) ≠ (2^1)/3
❌ Over-rounding: Don’t round too soon when estimating — use several decimal places for accuracy.
🤔 Bonus Fun: What if x * x * x is equal to 2?
This is a different but fascinating question.
It turns out that
x * x * x is equal to 2 is solved by x = √2
This is known as an infinite power tower, and while it’s not the same as x·x·x = 2, it shows how different forms of exponential and multiplicative math lead to unique constants.
🔗 Useful Links & Further Reading
🧮 Summary Table
| Term | Value or Info |
| x·x·x = 2 | x ≈ 1.259921 |
| Mathematical form | ∛2 or 2^(1/3) |
| Is it rational? | ❌ No — it’s irrational |
| Approx. cube root | Between 1.25 and 1.26 |
| Real-world use | Volume, density, geometry |
| Common mistake | Rounding or wrong root |
📌 Final Thoughts
The equation x·x·x = 2 teaches us more than just how to use a calculator—it opens the door to deeper mathematical understanding of roots, irrational numbers, and the history of problem-solving.
Whether you’re studying for school or just love math, this simple equation reminds us:
Even the smallest numbers can carry infinite depth.
X*X*X is equal to 2022
The equation X*X*X is equal to 2022 and presents an interesting mathematical puzzle. To solve for X, we need to find a number that, when multiplied by itself three times (cubed), gives a result close to 2022. Mathematically, this can be expressed as X³ = 2022. While the exact cube root of 2022 is not a whole number, it’s approximately 12.6348. Therefore, X is approximately 12.63. This calculation highlights the importance of using cube roots in solving cubic equations, making X*X*X = 2022 an intriguing math challenge.
Using known angles and trigonometric identities, you can derive the value of sin 15 degrees, an important trigonometric ratio. The exact value of sin 15 degrees is (√6 – √2)/4. This value is often used in solving various mathematical problems, especially in geometry and trigonometry. Understanding the sin 15 value can help simplify complex equations and is essential in many practical applications, including physics and engineering. Whether you’re studying for exams or working on technical projects, knowing how to calculate and use sin 15 degrees effectively is crucial for accurate results.