Trigonometry Formulas and Table (Class 10 to Class 12)
Trigonometry plays a crucial role in mathematics and physics. Below is a detailed collection of fundamental trigonometry formulas, including identities, function definitions, and a trigonometry table.
Fundamental Trigonometric Function Formulas for Class 10-12
The six primary trigonometric functions are:
- Sine (sin) = Opposite/Hypotenuse
- Cosine (cos) = Adjacent/Hypotenuse
- Tangent (tan) = Opposite/Adjacent
- Cosecant (csc) = 1/sin
- Secant (sec) = 1/cos
- Cotangent (cot) = 1/tan
Key Pythagorean Identities
- sin²θ + cos²θ = 1
- 1 + tan²θ = sec²θ
- 1 + cot²θ = csc²θ
Reciprocal Identities
- sinθ = 1/cscθ
- cosθ = 1/secθ
- tanθ = 1/cotθ
- cscθ = 1/sinθ
- secθ = 1/cosθ
- cotθ = 1/tanθ
Trigonometric Formulas for Sum and Difference of Angles
- sin(A ± B) = sinA cosB ± cosA sinB
- cos(A ± B) = cosA cosB ∓ sinA sinB
- tan(A ± B) = (tanA ± tanB) / (1 ∓ tanA tanB)
Double Angle and Half Angle Formulas
- sin(2A) = 2 sinA cosA
- cos(2A) = cos²A – sin²A
- tan(2A) = (2 tanA) / (1 – tan²A)
For half-angle formulas, use:
- sin(A/2) = ±√((1 – cosA) / 2)
- cos(A/2) = ±√((1 + cosA) / 2)
- tan(A/2) = ±√((1 – cosA) / (1 + cosA))
Trigonometry Table (Common Angles)
| Angle (θ) | sinθ | cosθ | tanθ | cotθ | secθ | cscθ |
| 0° | 0 | 1 | 0 | ∞ | 1 | ∞ |
| 30° | 1/2 | √3/2 | 1/√3 | √3 | 2/√3 | 2 |
| 45° | 1/√2 | 1/√2 | 1 | 1 | √2 | √2 |
| 60° | √3/2 | 1/2 | √3 | 1/√3 | 2 | 2/√3 |
| 90° | 1 | 0 | ∞ | 0 | ∞ | 1 |
Applications of Trigonometry
Trigonometry has numerous real-life applications, including:
- Engineering and Architecture
- Astronomy and Space Science
- Navigation and GPS
- Physics and Wave Mechanics
Trigonometry Cheat Sheet for Quick Revision
For a quick reference, you can use a Trigonometry Cheat Sheet that summarizes all important formulas, including:
- Basic trigonometric identities
- Reciprocal identities
- Sum and difference formulas
- Double and half-angle formulas
- Common trigonometric values
Download Trigonometry Formulas PDF
To help with your studies, you can download a Trigonometry Formulas PDF that includes all important formulas, tables, and identities in a well-structured format.
Conclusion
Mastering trigonometric formulas is essential for excelling in mathematics. This guide provides a structured approach for Class 10-12 students to understand and apply trigonometry effectively. Keep practicing and refer to this guide whenever needed!
Degrees of comparison are essential in English grammar, helping us express varying levels of comparison between adjectives. There are three degrees: positive, comparative, and superlative. The positive degree describes a quality without comparison (e.g., “tall”). The comparative degree compares two entities, often using “er” or “more” (e.g., “taller” or “more beautiful”). Lastly, the superlative degree highlights the highest degree among three or more entities, typically using “est” or “most” (e.g., “tallest” or “most beautiful”). Understanding these degrees of comparison enhances clarity and precision in communication. Use them effectively to enrich your language skills!
Parts of Speech With Examples
The parts of speech are the fundamental building blocks of English grammar. There are eight main parts: noun, pronoun, verb, adjective, adverb, preposition, conjunction, and interjection. Each part has a unique function in a sentence. For example, a noun represents a person or thing (e.g., “dog”), a verb describes an action (e.g., “run”), and an adjective modifies a noun (e.g., “beautiful”). An adverb modifies a verb, adjective, or another adverb (e.g., “quickly”). Understanding parts of speech with examples helps improve sentence structure and communication skills.

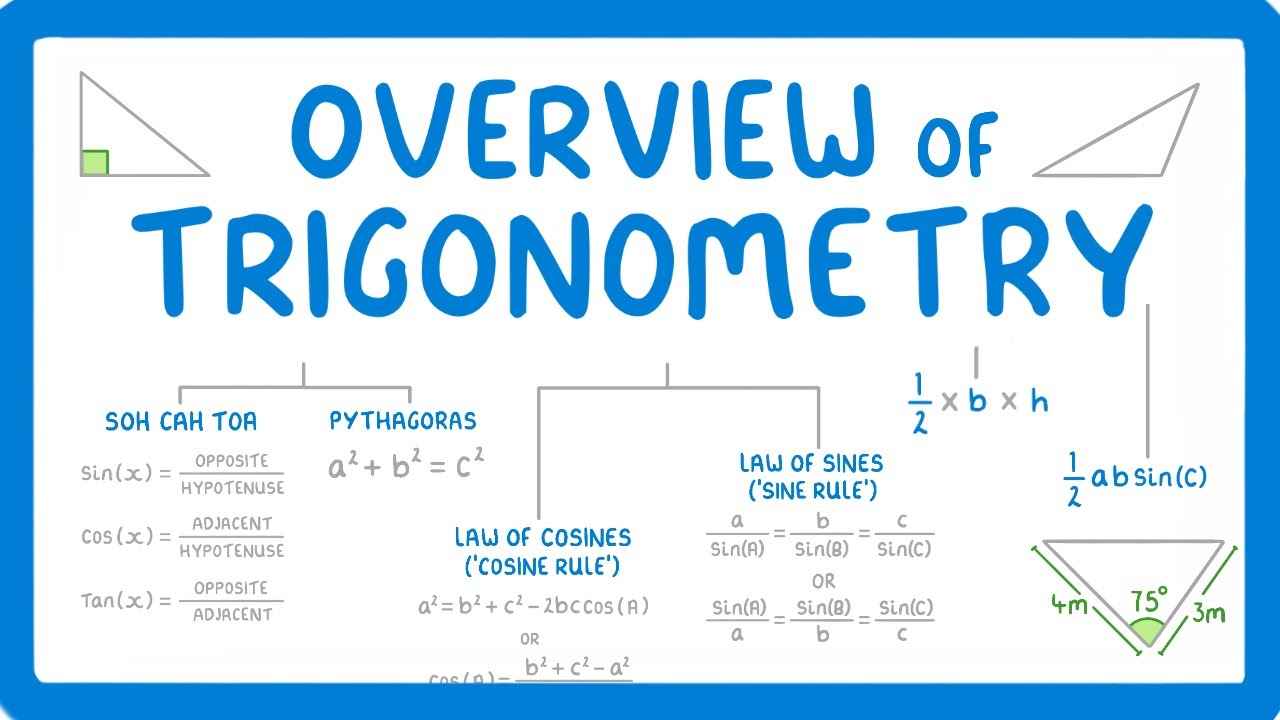




[…] Trigonometry formulas are fundamental tools used to solve problems involving triangles and angles. These formulas relate the angles of a triangle to the lengths of its sides, providing essential mathematical relationships in trigonometry. Key formulas include the sine, cosine, and tangent ratios, which are used to calculate angles and side lengths in right-angled triangles. Additionally, the Pythagorean theorem is a foundational concept that relates the lengths of the sides in a right triangle. Understanding and applying trigonometry formulas is essential in various fields such as engineering, physics, and mathematics, where precise calculations involving angles and distances are required. […]
[…] Trigonometry Formulas […]