Question: Find the roots of the quadratic equation x² – 11x + 28 = 0 by using the quadratic formula.
- 4 and 7
- -4 and -7
- 2 and 14
- -2 and -14
Answer: A. 4 and 7.
x² – 11x + 28 = 0 Solution:
The quadratic formula is: x = (-b ± √(b^2 – 4ac)) / 2a
- where a, b, and c are the coefficients of the quadratic equation. In this case, a = 1, b = -11, and c = 28.
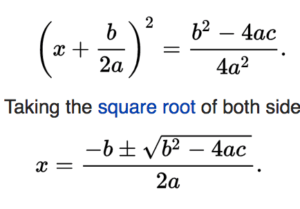
Substituting these values into the quadratic formula, we get:
x = (11 ± √(-11^2 - 4 * 1 * 28)) / 2 * 1- x = (11 ± √(121 – 112)) / 2
x = (11 ± √9) / 2- x = (11 ± 3) / 2
- x = 4 or 7
In conclusion, by applying the quadratic formula to the given equation, we find that the roots are x = 7 and x = 4, which matches option A.
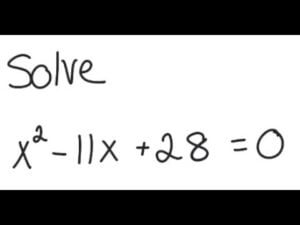
- By following this step-by-step solution, you have successfully solved the quadratic equation x² – 11x + 28 = 0 using the quadratic formula.
We can solve the equation using the quadratic formula, which is a general formula for solving quadratic equations. Great! I’ve been making significant progress in solving these quadratic equations problems. Let’s solve the equation. We can solve the equation using the quadratic formula, which is a general formula for solving quadratic equations.
Please visit us to learn more about more Questions and Information.




Thanks for me to find the solution of x² – 11x + 28 = 0.